0. 이전강의 내용 보충
0-1. 시멘틱(Semantics)
시멘틱에는 일련번호가 붙는데 0을 붙일경우 없는 것과 동일한 경우이다.
TEXCOORD = TEXCOORD0
COLOR = COLOR0
COLOR 시멘틱이 0~1범위의 시멘틱이라고 이전 강의 자료에 있었는데 그냥 COLOR로 0~1 범위에 한정되지 않고 그 이상도 담을수있다.
1-1. 동차 좌표계

2D공간과 3D공간의 크기를 제어하는 행렬은 대각선에 있다.
어떤 목적을 위해 한 차원의 좌표를 추가하여 표현을 하는 것을 동차 좌표계라고 한다.
우선 임의의 3차원 상의 점이 있다고 했을 때 축소, 확대 또는 회전 또는 이동에 관해서 행렬로 표현할 수 있다.
하지만 위의 모든 연산이 행렬의 곱으로서 표현되는 것은 아닌데, 특히 평행 이동 같은 경우는 곱셈으로
표현할 길이 보이지 않는다.
하지만 동차좌표가 되었을 때는 실제 3차원에서의 이동을 행렬 곱셈으로 표현할 수 있다.
실제 게임 개발에서는 개념이 쓰인다기보단 계산을 하기 용이해서 쓴다고 한다.
참조한 글 : 게임수학 - 동차좌표계, Homogeneous coordinates / by. 게임이 더 좋아

3D상에서 점과 벡터는 3개의 좌표로 명시되고, 같은 방법으로 명시되어 혼동을 야기한다.
속도와 방향을 가진 벡터 (x,y,z)와 좌표상의 점 (x,y,z) 을 동차좌표계에서는 네번째 좌표 (w)를 통해서 나타낸다.
벡터의 경우 w=0, 아닐경우 점이다.
이 링크에 점과 벡터가 0,1로 구분되는 것에 대해서 간단하게 설명이 되어있다.
그 외에도 투영변환이란 차원을 낮추는 변환에도 사용된다.
일반적으로 3차원이 2차원이 되는 변환을 말하며, 방향을 구분해야하는 필요성이 있다.
점이 어디에 위치하는 것이 중요한 것이 아니라 어느 방향에 있느냐가 중요해서인데,
그에 대해서는 위쪽의 참조글 링크로...
1-2. 행렬의 곱셈을 이용한 이동 행렬
3D공간에서 좌표의 이동은 덧셈으로 쉽게 이동이 가능하다.
하지만 벡터의 경우 원점에서 뻗어 나가는 벡터의 개념과 충돌한다.

위 행렬을 직접 곱해보면 ( x + dx , y + dy , z + dz , 1 ) 의 결과가 된다.
마지막 1은 사용하지 않고 버리면 된다.
이것의 원리는 차원을 늘려서 밀기(Shear) 변환 후 남는 차원을 버리는 방식이다.
이에 관해 자세히 설명된 링크는 아래와 같다.
이득우의 '상상하는 게임 수학' - 이동 행렬 (Translation Matrix)
1-3. 회전 변환과 회전 행렬 (2차원 회전)
기저 벡터가 회전함으로써 기준이 되는 벡터 공간이 회전된다.



기저 벡터가 회전함에 따라 결과적으로 공간 전체가 회전한 것.

1-4. 변환의 결합
변환 행령의 가장 강력한 점은 행렬을 결합할 수 있다는 점이다.
이동 행렬M, 회전 행렬R, 크기 행렬S가 있을 때 이동 후 회전 후 크기를 바꾸는 행렬의 곱셈 S˙R˙M을 계산한 T 행렬이
있다면 T는 이동,회전, 크기 변환을 모두 수행하는 복합 행렬이 된다.
이 과정을 변환의 결합이라고 한다.

차례대로 원점으로 (-0.5, -0.5) 이동하고 90도 회전이후 다시 본 위치로 (0.5, 0.5) 이동한다.
아래는 이미지로 된 보여지는 형태 위는 실제 행렬의 연산이다.

1-5. 오일러 회전
3차원 회전은 x,y,z 세 개의 축에 대한 오일러 회전이다.

3차원 공간의 회전 변환은 각 축의 회전 행렬을 원하는 순서대로 곱해서 만들어진다.


Roll은 Z축 중심 회전이고 x,y 평면 회전이다.


Pitch는 X축 중심 회전으로 y,z 평면 회전이다.
Yaw는 y축 중심 회전으로 x,z 평면 회전이다.


다음 링크에서 공업 수학에 관점으로 설명된 내용을 볼 수 있다. 그외에도 드론을 통해 설명된 자료도 있다.
1-X. 아핀 공간, 아핀 변환 (참고자료 / 접은 글)

벡터나 벡터 공간은 방향과 힘의 크기로 나타낼 수 있으나 직접적으로 눈에 보이는 개념이 아니다.
“물체를 표현하려면 어떤 것이 필요할까? 가장 기본적인 요소를 꼽자면 점을 들 수 있다. 점이 모여 선이 되고, 선이 모여 평면이 되고 평면이 모여서 입체가 된다. 이렇게 무언가를 형상화 시키기 위해 필요한 추가 요소를 정의한 공간을 아핀 공간이라고 하며, 아핀 공간에서 새롭게 정의한 요소는 점(point)이다.
아핀 공간은 기존 벡터 공간 점이라는 추상적인 개념을 추가해서 창조한 새로운 개념의 공간인 것이다.”
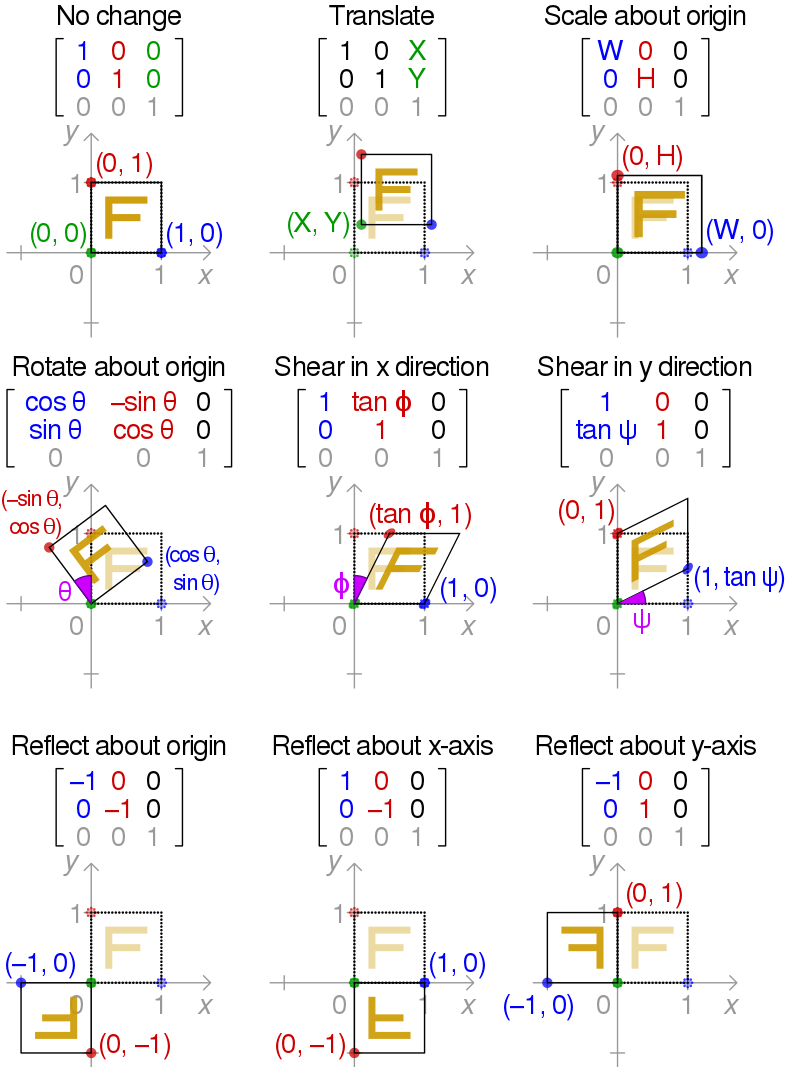
아핀 변환이란 공간에서 도형의 성질을 유지한 채 공간이 변형되는 함수를 뜻한다.
그 외 참고할만한 글
아핀 공간과 벡터 공간의 차이점 / by. Gyong
어떤 점이 원점인지 잊어버린 후 벡터 공간에 남겨진 것은 아핀 공간이다 라고 하는데...
1-6. 역행렬


역행렬은 -1 첨자를 사용해서 표기를 한다.

역행렬의 특징 중 하나는 행렬과 역행렬을 곱하면 항등 행렬이 된다는 점이다.
2-1. 벡터의 MVP 변환

좌표 공간의 종류와 변환을 이해하기 위한 이미지 (하단) 설명된 글 (링크)


2-2. View -> Projection 변환 = Clip Space

원근감이 반영된 좌표공간으로 변환되어 가까이 있는 오브젝트는 x방향으로 훨씬 커지고 멀리 있는 오브젝트는 작아졌다.
결과적으로 Vertex의 값이 달라졌다.
2-3. 여러 단계의 공간 변화를 거치는 이유
한번에 최종 변환도 가능하다.
하지만 셰이더 코드를 만들다보면 각각의 공간 좌표계가 필요할 때가 있다.
아래는 버텍스 셰이더의 공간 변환을 여러 단계로 나눈 뒤 각각의 단계에서 버텍스 이동에 개입한 예제이다.
L 오브젝트 공간
M 월드 공간
V 뷰 공간 ( 겜 카메라 씬 카메라 ) [ Z 원근 ] [ W 카메라 니어 파? ]
P 클립 공간
에 개입하여 버텍스 이동을 진행한 이미지이다.
셰이더 코드 일부 발췌
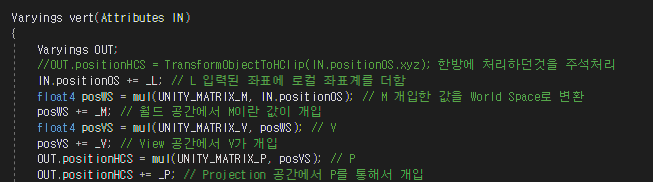




View공간의 Z값이 부호가 바뀌어 Projection공간의 W값으로 옮겨감

Projection의 W값은 NDC공간으로 갈때 나누는데 사용된다.
2-X. positionHCS ( Homogeneous Clip Space )
“기존 공간에 무한대 개념이 추가된 공간을 사영 공간(projective space)이라고 하며, 사영 공간이 사용하는 무한대 개념까지 수용하는 좌표계를 동차 좌표계(homogeneous coordinate)라고 한다.”
프로젝션 변환 행렬은 수학적으로 깊이 들어가므로 다루지 않음.
시연 :
Assets > CK_GGE > CustomShader > BRDF > BRDFTest 씬 > MVP_Cube
재질의 P 값인 클립공간에서 z 조절과 w 조절을 비교해보자
- z 조절은 원근감이 고정된 채 거리가 달라진다.
- w 조절은 카메라로부터 실제 거리가 달라진다.
(참고) What is clip space?
‘절단 공간’ 이라고도 부름
2-4. 공간 변환 함수를 사용하는 이유
유니티가 제공하는 mvp행렬을 곱하지 않고 함수를 사용하는 이유가 있는데,
함수를 사용하게되면 전처리지시어에 따라서 대상 플랫폼에 상태에 따라서 다른 연산을 할 수 있도록 다양성을 제공한다.
이점에서 행렬만 곱하는 것과 차이가 생긴다.

즉
mul(UNITY_MATRIX_MVP, positionOS)로 사용하는 것과 UnityObjectToClipPos(positionOS)로 사용하는 것은
같지만 다른 것이다.
2-5. 클립 공간 ( Clip Space ) 의 특징
카메라 종횡비에 영향을 받는다.

Z 값은 카메라의 Far~Near을 기준으로 0~1 값이다.
W 값은 카메라로부터의 실제 거리로 클립공간 이외의 공간에서는 w값이 1이다.
이후 ndc좌표로 변환될때 나누는 값으로 사용된다. ( 나누면 카메라에 가까울 수록 커진다. )
2-6. 정규 기기 공간(Normalized Device Coordinates)
화면의 종횡비에 상관없이 가운데가 0이며 가장자리 끝이 1크기를 가진다.

OpenGL과 DirectX와 축체계가 다르다.

2-7. 스크린 공간 (Screen Space)
0~1의 UV공간으로 스크린 공간 또한 OpenGL과 DirectX의 축체계가 다르다.

2-8. mul함수
HLSL에서 행렬을 곱할때 mul함수를 사용하였는데, 해당 함수는 거의 모든 데이터형을 인수로 받는다.

2-X 행렬 (Matrix) 관련 메모
DirectX와 HLSL간의 행렬순서와 연산 - 행렬, 행우선과 열우선
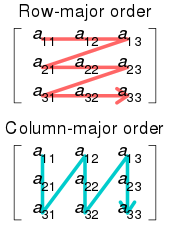
mul 함수에서 앞 뒤 순서를 바꾸면? - 전치행렬과 같은 결과
(열우선 행우선 계산 순서가 바뀐다고 하는듯)

mul 연산에 사용하는 float4에서 w 값의 역할 - w를 0으로 하면 회전만 하고 이동 안함. 1로 하면 이동도 한다. 그래서 이동 계산이 필요 없는 벡터 변환은 mul((float3x3)matrix, float3) 을 사용함
Unity - shader의 World matrix(unity_ObjectToWorld)를 수작업으로 구성
Projection 변환 행렬을 이해하려면 - ‘투영 변환 행렬’ 키워드로 검색
3-X. 아웃라인 셰이더의 원리
이 포스트는 청강문화수업대학교 게임스쿨 '게임그래픽엔진심화' 수업에 대해서 복습진행을 위해 작성된 포스트입니다.
글 작성을 위해 교수님의 수업자료 및 내용을 다수 참고하였습니다.
외부에서 발췌, 참고한 글의 내용의 경우 해당 내용에 링크를 포함하여 작성하였습니다.
'유니티' 카테고리의 다른 글
| 14강 (0) | 2022.06.20 |
|---|---|
| 13강 (14주차 진행) (0) | 2022.06.09 |
| 11강(12주차진행) (0) | 2022.05.25 |
| 10강 (11주차) (0) | 2022.05.18 |
| 9강 (10주차) (0) | 2022.05.10 |

